This analysis was inspired from Twitter’s interesting analysis of tweet lengths published on Twitter’s engineering blog. The gist of the analysis was this:
English language tweets display a roughly log-normal distribution of character counts, except near the 140-character limit - an evidence of cramming thoughts to fit 140 characters.
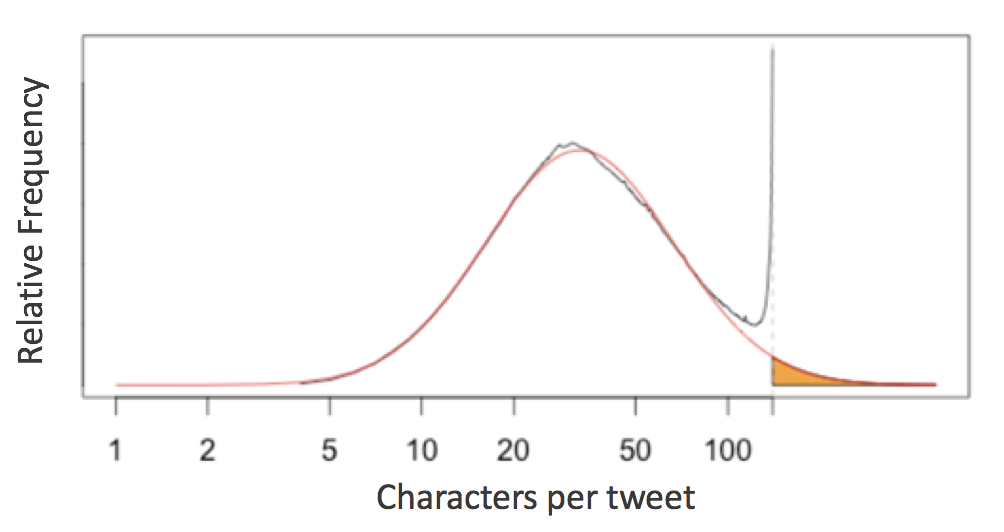
This prompts the question of the 79-character line limit suggested by Python’s PEP8 style guide:
Limit all lines to a maximum of 79 characters.
Jake VanderPlas invistigated this for scientific python packages. Let’s see how it affects FluidDyn packages!
Counting Lines in fluiddyn¶
To take a look at this, we first need a way to access all the raw lines of code in any Python package. In a standard system architecture, if you have installed a package you already have the Python source stored in your system.
import fluiddyn
With this in mind, we can use the os.walk function to write a quick generator function that will iterate over all lines of Python code in a given package:
# Python 3.X
import os
def iter_lines(module):
"""Iterate over all lines of Python in module"""
for root, dirs, files in os.walk(module.__path__[0]):
for filename in files:
if filename.endswith('.py'):
with open(os.path.join(root, filename)) as f:
yield from f
This returns a generator expression that iterates over all lines in order; let's see how many lines of Python code NumPy contains:
lines = iter_lines(fluiddyn)
len(list(lines))
11340
Given this we can find the lengths of all the lines and plot a histogram:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
plt.style.use('ggplot')
lengths = [len(line) for line in iter_lines(fluiddyn)]
plt.hist(lengths, bins=np.arange(max(lengths)), histtype='step', linewidth=1);
The distribution is dominated by lines of length 1 (i.e. containing only a newline character): let's go ahead and remove these, and also narrow the x limits:
lengths = [len(line) for line in iter_lines(fluiddyn) if len(line) > 1]
plt.hist(lengths, bins=np.arange(125), histtype='step', linewidth=1);
Now this is looking interesting!
Cleaning the Distribution¶
The first feature that pops out to me are the large spikes between 0 and 20 characters. To explore these, let's look at the lines that make up the largest spike:
np.argmax(np.bincount(lengths))
27
We can use a list comprehension to extract all lines of length 13:
lines27 = [line for line in iter_lines(fluiddyn) if len(line) == 27]
len(lines27)
237
There are 237 lines in fluiddyn with a length of 27 characters. It's interesting to explore how many of these short lines are identical.
The Pandas value_counts function is useful for this:
import pandas as pd
pd.value_counts(lines27).head(10)
if __name__ == '__main__':\n 48
from builtins import range\n 15
nb_cores_per_node = 16\n 3
sys.stdout.flush()\n 3
except ValueError:\n 3
print(*args, **kwargs)\n 2
for serie in self:\n 2
return self.shapeK\n 2
except AttributeError:\n 2
self.coef_norm = n\n 2
dtype: int64
It’s clear that many of these duplicates are just a manifestation of if __name__ == '__main__': line and some imports from python-future package recurring at the beginning and the end of many modules.
lengths = [len(line) for line in set(iter_lines(fluiddyn))]
plt.hist(lengths, bins=np.arange(125), histtype='step', linewidth=1);
That's a much cleaner distribution!
Comparison Between Packages¶
In order to aid comparison between packages, let's quickly refactor the above histogram code into a function that we can re-use. In addition, we'll add a vertical line at the PEP8's maximum character count:
def hist_linelengths(module, ax):
"""Plot a histogram of lengths of unique lines in the given module"""
lengths = [len(line.rstrip('\n')) for line in set(iter_lines(module))]
h = ax.hist(lengths, bins=np.arange(125) + 0.5, histtype='step', linewidth=1.5)
ax.axvline(x=79.5, linestyle=':', color='black')
ax.set(title="{0} {1}".format(module.__name__, module.__version__),
xlim=(1, 100),
ylim=(0, None),
xlabel='characters in line',
ylabel='number of lines')
return h
Now we can use that function to compare the distributions for a number of well-known scientific Python packages:
%%capture --no-display
import fluiddyn, fluidsim, fluidfft, fluidimage, fluidlab, fluidcoriolis
modules = [fluiddyn, fluidsim, fluidfft, fluidimage, fluidlab, fluidcoriolis]
fig, ax = plt.subplots(2, 3, figsize=(14, 6), sharex=True)
fig.subplots_adjust(hspace=0.2, wspace=0.2)
for axi, module in zip(ax.flat, modules):
hist_linelengths(module, ax=axi)
for axi in ax[0]:
axi.set_xlabel('')
for axi in ax[:, 1:].flat:
axi.set_ylabel('')
The results here are quite interesting: similar to Twitter’s tweet length analysis, we see that each of these packages have a somewhat smooth distribution of characters, with a “cutoff” at or near the 79-character PEP8 limit! There is a reasonable adherence to PEP8 standards, but unlike the results from Jake’s analysis of other scientific pacakges, there are no recognizable “bumps” near the 79-character limit. fluidfft has the most cleanest tail with absolutely 0 lines with above 79 characters - a luxury of being the newest package.
But one package stands out: fluidsim displays some noticeable spikes at a few intermediate line lengths; let’s take a look at these:
lines = set(iter_lines(fluidsim))
counts = np.bincount([len(line) for line in lines])
np.argmax(counts)
50
The large spike reflects the approximately 300 lines with exactly 50 characters; printing some of these and examining them is interesting:
[line for line in lines if len(line) == 50][:10]
["def load_bench(path_dir, solver, hostname='any'):\n",
' subcommand = compute_name_command(module)\n',
" it = group_state_phys.attrs['it']\n",
' freq_complex = np.empty_like(state_spect)\n',
' shape_variable=(33, 18),\n',
' sim.oper.KX[ikx, iky],\n',
" z_fft = self.state_spect.get_var('z_fft')\n",
' Fy_reu = -urx * px_etauy - ury * py_etauy\n',
'=================================================\n',
' PZ2_fft = (abs(Frot_fft)**2)*deltat/2\n']
Maybe not so interesting after all, just a coincidence! :)
Modeling the Line Length Distribution¶
Following the Twitter character analysis, let's see if we can fit a log-normal distribution to the number of lines with each character count. As a reminder, the log-normal can be parametrized like this:
$$ LogNorm(x; \mu, \sigma) = \frac{1}{x \sigma \sqrt{2\pi}} \exp\left(-\frac{[\log(x) - \mu]^2}{2\sigma^2}\right) $$
Here $x$ is the number of counts, $\exp(\mu)$ is the median of the peak of the distribution, and $\sigma^2$ controls the distribution's width.
We can implement this using the lognorm distribution available in scipy:
from scipy import stats
def lognorm_model(x, amplitude, mu, sigma):
return amplitude * stats.lognorm.pdf(x, scale=np.exp(mu), s=sigma)
x = np.linspace(0, 100, 1000)
plt.plot(x, lognorm_model(x, 1000, 3.5, 0.7));
That seems like an appropriate shape for the left portion of our datasets; let's try optimizing the parameters to fit the counts of lines up to length 50:
from scipy import optimize
counts, bins, _ = hist_linelengths(fluiddyn, ax=plt.axes())
lengths = 0.5 * (bins[:-1] + bins[1:])
def minfunc(theta, lengths, counts):
return np.sum((counts - lognorm_model(lengths, *theta)) ** 2)
opt = optimize.minimize(minfunc, x0=[10000, 4, 1],
args=(lengths[:50], counts[:50]),
method='Nelder-Mead')
print("optimal parameters:", opt.x)
plt.fill_between(lengths, lognorm_model(lengths, *opt.x), alpha=0.3, color='gray');
optimal parameters: [6.53825230e+03 3.68332005e+00 4.59205976e-01]
Seems like a reasonable fit! From this, you could argue (as the Twitter engineering team did) that the line lengths might "naturally" follow a log-normal distribution, if it weren't for the artificial imposition of the PEP8 maximum line length.
For convenience, let's create a function that will plot this lognormal fit for any given module:
def lognorm_model(x, theta):
amp, mu, sigma = theta
return amp * stats.lognorm.pdf(x, scale=np.exp(mu), s=sigma)
def minfunc(theta, lengths, freqs):
return np.sum((freqs - lognorm_model(lengths, theta)) ** 2)
def lognorm_mode(amp, mu, sigma):
return np.exp(mu - sigma ** 2)
def lognorm_std(amp, mu, sigma):
var = (np.exp(sigma ** 2) - 1) * np.exp(2 * mu + sigma ** 2)
return np.sqrt(var)
def hist_linelengths_with_fit(module, ax, indices=slice(50)):
counts, bins, _ = hist_linelengths(module, ax)
lengths = 0.5 * (bins[:-1] + bins[1:])
opt = optimize.minimize(minfunc, x0=[1E5, 4, 0.5],
args=(lengths[indices], counts[indices]),
method='Nelder-Mead')
model_counts = lognorm_model(lengths, opt.x)
ax.fill_between(lengths, model_counts, alpha=0.3, color='gray')
# Add text describing mu and sigma
A, mu, sigma = opt.x
mode = np.exp(mu - sigma ** 2)
ax.text(0.22, 0.15, 'mode = {0:.1f}'.format(lognorm_mode(*opt.x)),
transform=ax.transAxes, size=14)
ax.text(0.22, 0.05, 'stdev = {0:.1f}'.format(lognorm_std(*opt.x)),
transform=ax.transAxes, size=14)
return opt.x
Now we can compare the models for each package:
modules = [fluiddyn, fluidsim, fluidfft, fluidimage, fluidlab, fluidcoriolis]
fig, ax = plt.subplots(2, 3, figsize=(14, 6), sharex=True)
fig.subplots_adjust(hspace=0.2, wspace=0.2)
fits = {}
for axi, module in zip(ax.flat, modules):
fits[module.__name__] = hist_linelengths_with_fit(module, ax=axi)
for axi in ax[0]:
axi.set_xlabel('')
for axi in ax[:, 1:].flat:
axi.set_ylabel('')
It is also interesting to use these summary statistics as a way of describing the "essence" of each package, in order to compare them directly:
ha = {'fluidfft': 'right', 'fluidlab': 'right', 'pandas': 'right'}
va = {'fluidfft': 'top'}
for name, fit in sorted(fits.items()):
mode = lognorm_mode(*fit)
std = lognorm_std(*fit)
plt.plot(mode, std, 'ok')
plt.text(mode, std, ' ' + name + ' ', size=14,
ha=ha.get(name, 'left'), va=va.get(name, 'bottom'))
plt.xlabel('mode of model', size=14)
plt.ylabel('std. deviation of model', size=14);
plt.xlim(27, 45);
plt.ylim(21, 41);
This notebook originally appeared as a post on the blog Pythonic Perambulations. The code content is MIT licensed.
This modified post was written entirely in the Jupyter notebook. You can download this notebook, or see a static view on nbviewer.